11 Sequences Mr. Guesto
Clear explanation on the differences between an arithmetic and geometric sequence.

Arithmetic vs Geometric 5 Key Differences, Pros & Cons, Examples Difference 101
See more videos at:http://talkboard.com.au/In this video, we look at the difference between arithmetic and geometric sequences and some of their properties.

Arithmetic vs Geometric Sequences YouTube
Arithmetic sequences involve a constant difference between consecutive terms, while geometric sequences involve a constant ratio between consecutive terms. Key Takeaways Arithmetic sequence is a sequence where each term is obtained by adding a constant to the preceding term.

PPT Introduction to Geometric Sequences and Series PowerPoint Presentation ID6599086
What is the difference between an arithmetic sequence and a geometric sequence? In an arithmetic sequence, we add the same number to each term in order to get the next term in the sequence. In a geometric sequence, we multiply each term by the same number in order to get the next term. How do we construct arithmetic sequences?

SOLUTION Venn diagram of arithmetic and geometric Studypool
Geometric Sequences. A sequence is called geometric if the ratio between successive terms is constant. Suppose the initial term a0 a 0 is a a and the common ratio is r. r. Then we have, Recursive definition: an = ran−1 a n = r a n − 1 with a0 = a. a 0 = a. Closed formula: an = a ⋅ rn. a n = a ⋅ r n. Example 2.2.3 2.2. 3.

Category 1 Arithmetic and Geometric Sequences YouTube
In an arithmetic sequence, each term is the previous term plus the constant difference. So, you add a (possibly negative) number at each step. In a geometric sequence, though, each term is the previous term multiplied by the same specified value, called the common ratio.

Difference between Arithmetic and Geometric Sequence
6: Sequences and Series
5 Important Difference between Arithmetic and Geometric Sequence Core Differences
1 Answer Sorted by: 4 Geometric and arithmetic are two names that are given to different sequences that follow a rather strict pattern for how one term follows from the one before. An arithmetic sequence is characterised by the fact that every term is equal to the term before plus some fixed constant, called the difference of the sequence.

Question Video Determining Whether a Given Sequence Is Arithmetic or Geometric Nagwa
Arithmetic Sequence refers to a list of numbers, in which the difference between successive terms is constant. To put simply, in an arithmetic progression, we add or subtract a fixed, non-zero number, each time infinitely. If a is the first member of the sequence, then it can be written as: a, a+d, a+2d, a+3d, a+4d.. where, a = the first term

11.2 and 11.3 Arithmetic and Geometric Sequence
An arithmetic Sequence is a set of numbers in which each new phrase differs from the previous term by a fixed amount. Geometric Sequence is a series of integers in which each element after the first is obtained by multiplying the preceding number by a constant factor.

Arithmetic Sequence vs Geometric Sequence YouTube
The biggest difference between arithmetic vs geometric series lies in the type of difference between the consecutive terms. The consecutive terms of an arithmetic sequence have a constant difference while the terms of a geometric difference are in a constant ratio. Let's take a closer look at arithmetic vs. geometric here: Table of Contents

Arithmetic vs Geometric Sequence The Key Difference You Should Know
Arithmetic progression is a sequence of numbers in which the difference of any two adjacent terms is constant. The constant difference is commonly known as common difference and is denoted by d. Examples of arithmetic progression are as follows: Example 1: 3, 8, 13, 18, 23, 28 33, 38, 43, 48

K 12 GRADE 10 DIFFERENCE BETWEEN ARITHMETIC AND GEOMETRIC SEQUENCE YouTube
Geometric Sequences. A sequence is called geometric if the ratio between successive terms is constant. Suppose the initial term a0 a 0 is a a and the common ratio is r. r. Then we have, Recursive definition: an = ran−1 a n = r a n − 1 with a0 = a. a 0 = a. Closed formula: an = a⋅rn. a n = a ⋅ r n.
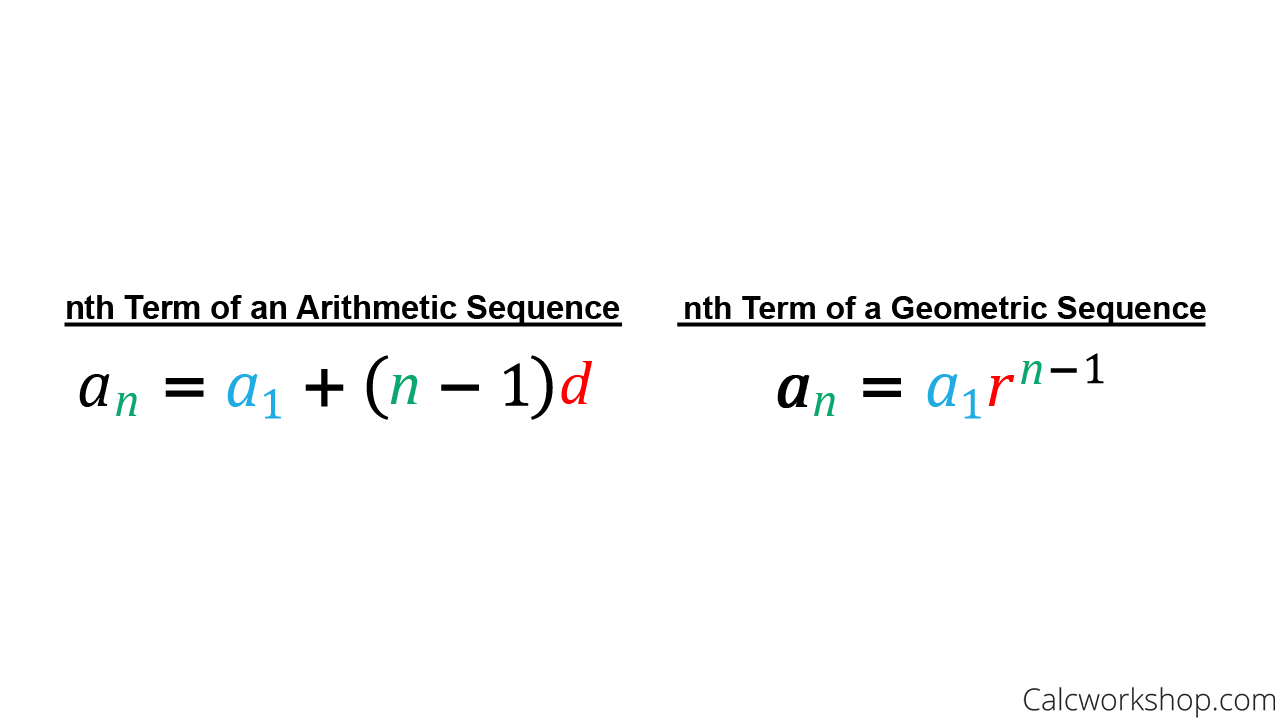
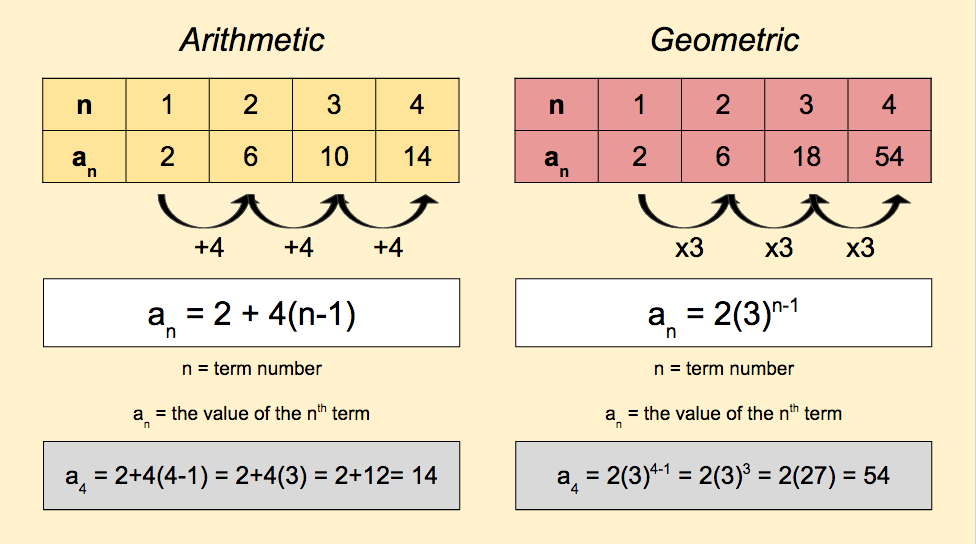
Arithmetic and Geometric Sequences (17+ Amazing Examples)
1 − 1) d an = the term in the sequence you are trying to find (n represents the desired term number) a1 = the first term in the sequence d = the common difference Example: What is the 10th term of the following sequence? 1, 5, 9, 13,. a = 10 1 + (10 − 1)4 = 1 + 9 ⋅ 4 = 1 + 36 = 37 So the 10th term of this sequence is 37.

What is the difference between Arithmetic and Geometric Sequences. Example YouTube
An arithmetic sequence has a constant difference d between consecutive terms. The same number is added or subtracted to every term, to produce the next one.. Notice how the number of people at every step forms a geometric sequence arithmetic sequence triangle number, with common ratio : 1, 3 ×3,.
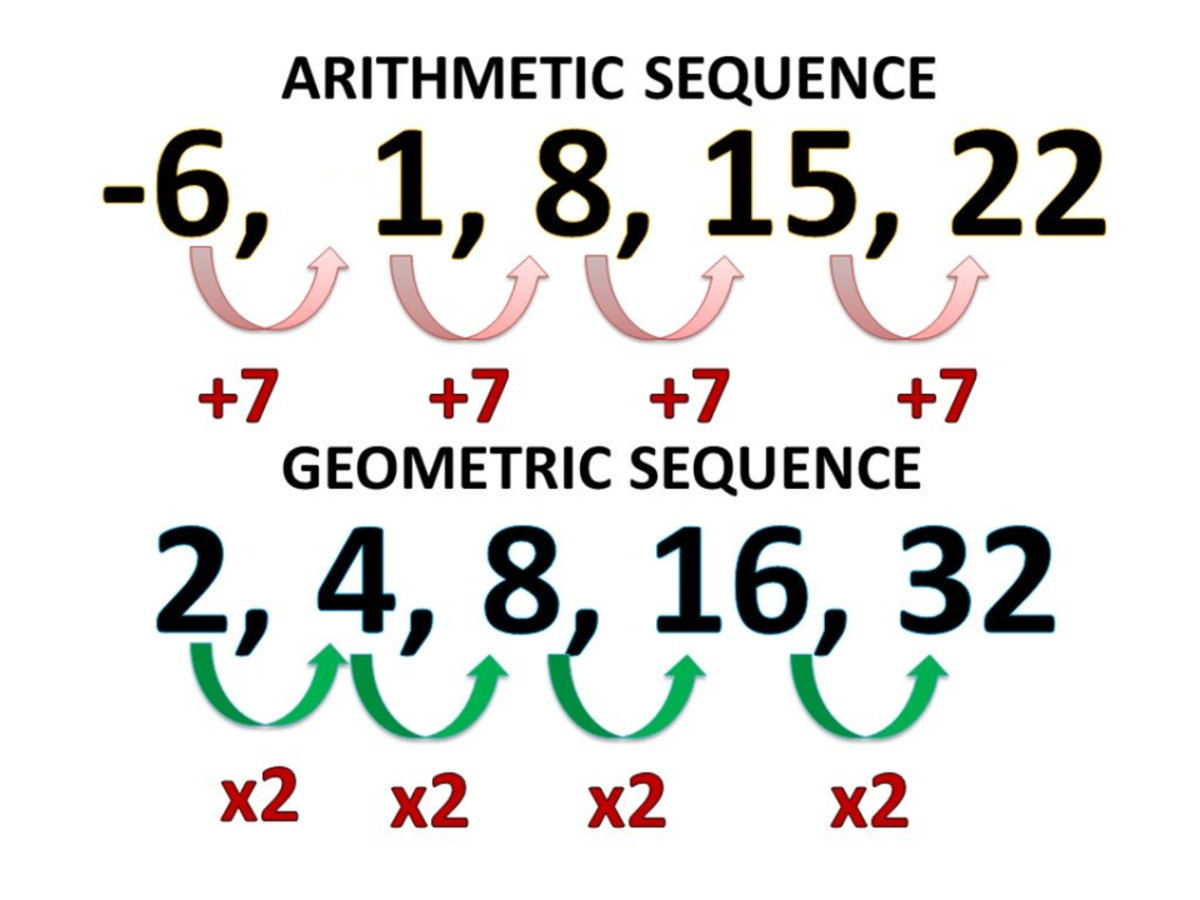
How to Find the General Term of Sequences Owlcation
The prime difference between an Arithmetic and a Geometric Sequence is that in an arithmetic sequence, the numbers are set in a manner where the difference between the two consecutive terms remains fixed. In the geometric sequence, there is a fixed ratio between any of the successive terms.