
Feynman’s integral tricks for solving challenging integration problem. YouTube
A crazy approach to the gaussian integral using Feynman's technique - YouTube © 2023 Google LLC Here's another video on evaluating the gaussian integral using the Leibniz rule; the.

Solve Integral by using Feynman's Trick (Leibniz integral rule) (1e^(x^2))/x^2 from 0 to
Welcome to the awesome 12-part series on the Gaussian integral. In this series of videos, I calculate the Gaussian integral in 12 different ways. Which metho.

A Crazy Integral (Feynman's Trick) [Difficulty 4] YouTube
Feb 23, 2022 2 Graphical representation of the Gaussian Integral (Image: Wikimedia Commons) The first time I came across the Gaussian integral, also known as the Euler-Poisson integral,.

Feynman's Integration Trick YouTube
The double integrals are surface integrals over the surface Σ, and the line integral is over the bounding curve ∂Σ. Higher dimensions. The Leibniz integral rule can be extended to multidimensional integrals. In two and three dimensions, this rule is better known from the field of fluid dynamics as the Reynolds transport theorem:

Variant Gaussian Integral e^(a x^2)cos(b x), from 0 to infinity, General Case, Feynman's trick
Among a few other integral tricks and techniques, Feynman's trick was a strong reason that made me love evaluating integrals, and although the technique itself goes back to Leibniz being commonly known as the Leibniz integral rule, it was Richard Feynman who popularized it, which is why it is also referred to as Feynman's trick.

Feynman's Technique This is the greatest integration method of All Time YouTube
On its last page, the author, Mr. Anonymous, left several exercises without any hints, one of them is to evaluate the Gaussian integral ∫∞ 0 e−x2 dx = π−−√ 2 ∫ 0 ∞ e − x 2 d x = π 2 using this parametrization trick. I had been evaluating it through trial and error using different paramatrizations, but no luck so far.

Feynman's Trick MIT Integration Bee (23.5) YouTube
Feynman's Favorite Trick 3.1 Leibniz's Formula The starting point for Feynman's trick of 'differentiating under the integral sign,' mentioned at the end of Chap. 1, is Leibniz's formula. If we have the integral IðÞ¼α ð bðÞα aðÞα fx,ðÞα dx where α is the so-called parameter of the integral (not the dummy variable of

Solving Gaussian Integral (integration of gaussian function) using Feynman’s Method. YouTube
However, as we will see, utilizing Feynman's path-integral formulation of quantum mechanics, Gaussian integrals are also central for computation in quantum statistical mechanics and more generally in quantum field theory. A. one degree of freedom Let us start out slowly with standard, scalar, one-dimension Gaussian integrals Z 0(a) = Z ∞.

Visual proof of Feynman's Trick Leibniz Integral rule YouTube
This is known as the Gaussian integral, after its usage in the Gaussian distribution, and it is well known to have no closed form. However, the improper integral. I = \int_0^\infty e^ {- x^2} \, dx I = ∫ 0∞ e−x2 dx. may be evaluated precisely, using an integration trick. In fact, its value is given by the polar integral.

∫sin(√3 ln(x))/ln(x) [0, 1]. Solving challenging integration problem using Feynman’s Integral
Feynman's Favorite Trick 3.1 Leibniz's Formula The starting point for Feynman's trick of 'differentiating under the integral sign,' mentioned at the end of Chap. 1, is Leibniz's formula. If we have the integral IðÞ¼α ð bðÞα aðÞα fxðÞ;α dx where α is the so-called parameter of the integral (not the dummy variable of

Integral of ln(x) with Feynman's trick! YouTube
Kasper Müller · Follow Published in Cantor's Paradise · 10 min read · Jan 18, 2022 -- 7 Richard Feynman in 1959. Picture is from Wikimedia Commons. Differentiation and integration are two sides of the same coin. Sometimes we call that "coin" calculus.
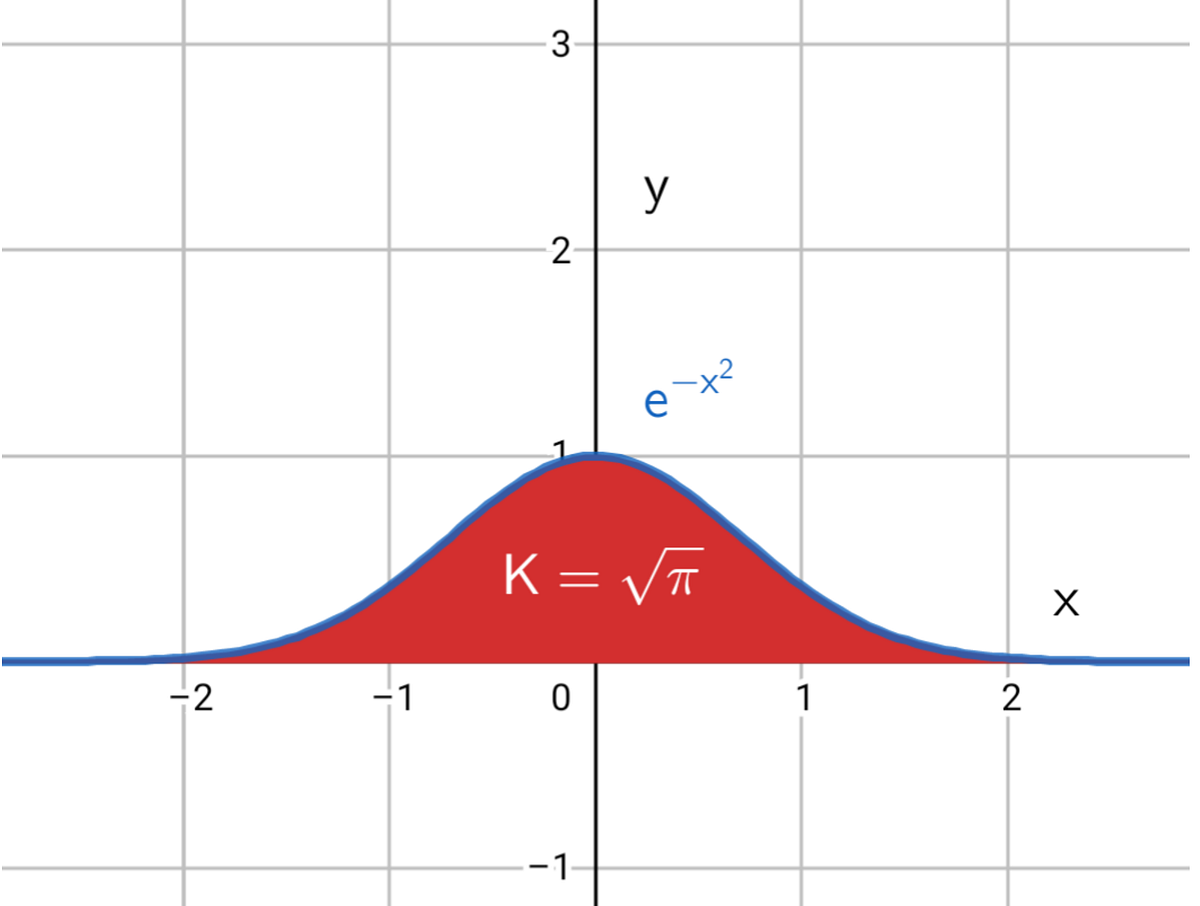
Solving the Gaussian Integral using the Feynman Integration method by Rthvik Raviprakash Medium
Find the Integral x^2e^-x^2 (x squared multiplied by e raised to x square) using a simple,fast and interesting method using Gaussian integral and differentia.
Gaussian integral using Feynman’s technique Add just a bit of pi
The trick of inverting Feynman's trick by integrating the integral of interest to make a double integral and then reversing the order of integration is introduced. The Cauchy-Schlӧmilch transformation is stated, derived, and used to evaluate some interesting variations of the probability integral. Download chapter PDF 3.1 Leibniz's Formula

Learning Effectively With the Feynman Technique (The Complete Guide) LifeHack
The integral is easily evaluated: F (t) = 1 t for all t > 0. Differentiating F with respect to t leads to the identity: Taking further derivatives yields: Which immediately implies the formula: The right hand side is the famous Gamma function, and does not depend on n being an integer.

Lect_1 FEYNMAN PATH INTEGRAL YouTube
2 Answers Sorted by: 1 If your heart's set on a solution using Feynman's trick, note ∫∞ 0re − ar2dr = 1 2a ∫∞ 0r3e − ar2dr = 1 2a2. So − I(a)I′(a) = ∫R2x2e − ar2dxdy = ∫2π 0 cos2θdθ∫∞ 0r3e − ar2dr = π 2a2.

Solving a nice integral via Feynman's trick YouTube
1. DERIVATION OF THE GAMMA FUNCTION An old problem is to extend the factorial function to non-integer arguments. This was resolved by Euler, who discovered two formulas for n! (one an integral, the other an infinite product) which make sense even when n is not an integer.