
16. Cauchy's Theorem and Cauchy's Integral Formula Problem1 Complete Concept YouTube
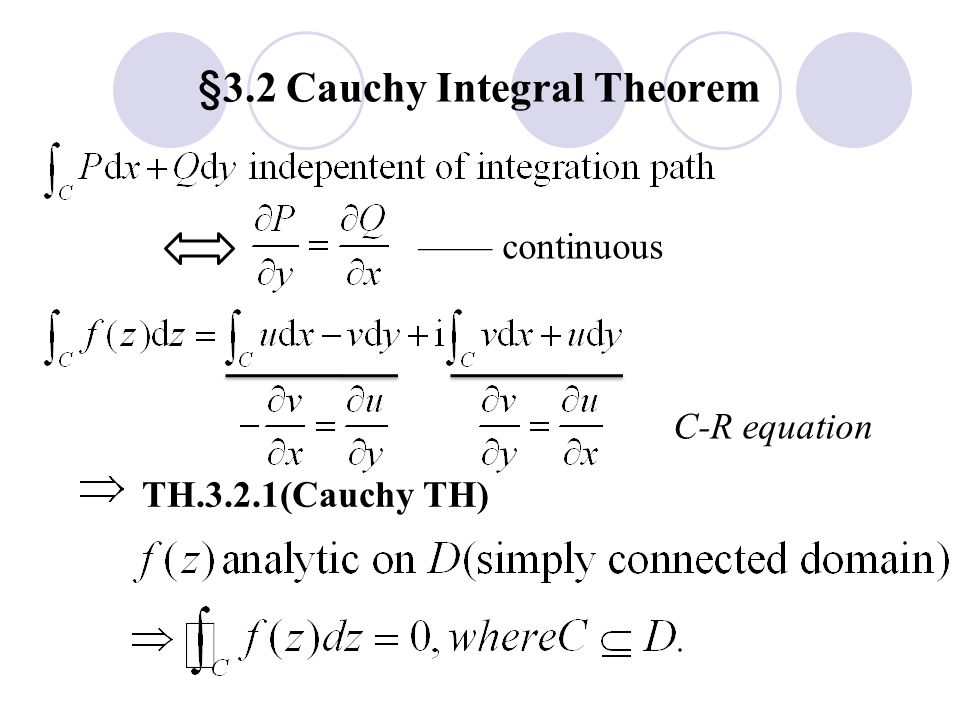
Chapter & Page: 15-4 Cauchy Integral Theorems and Formulas and, thus, equation (15.2) reduces to I C f (z)dz = − ZZ S 0dA + i ZZ S 0dA = 0 . Since every closed curve can be decomposed into a bunch of simple closed curves, the above

Cauchy's Integral Formula/Cauchy's Differentiation Formula used to Integrate e^z/(z 1)^5 YouTube
5.2: Cauchy's Integral Formula for Derivatives Cauchy's integral formula is worth repeating several times. So, now we give it for all derivatives f(n)(z) of f . This will include the formula for functions as a special case. 5.3: Proof of Cauchy's integral formula; 5.4: Proof of Cauchy's integral formula for derivatives

complex analysis How to apply cauchy integral formula. Mathematics Stack Exchange
This page titled 5.2: Cauchy's Integral Formula for Derivatives is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Jeremy Orloff (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.

Cauchy's integral formula
Cauchy's integral formula still holds in that case. The proof is left for the reader. Examples Let Cbe the unit circle centered in 0 and traversed in the counterclockwise direction. Z C cosz z dz= 2ˇin(C;0)cos(0) = 2ˇi Let be the arc composed of the line segment [ 2 p 3 ;2 p 3] along the real axis, and the upper half of

cauchy integral theorem Liberal Dictionary
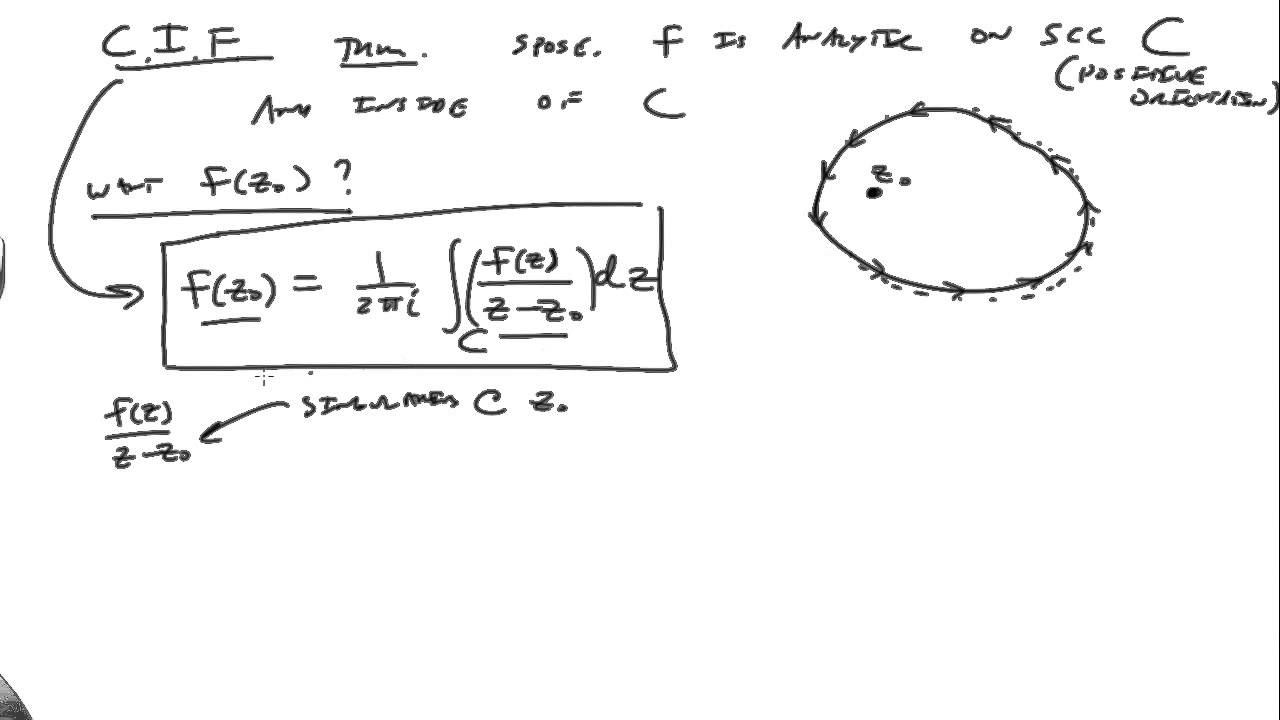
Cauchy's Integral Formula. Let z0 ∈ C and r > 0. Suppose f (z) is analytic on the disk. = {z : |z − z0| < r}. Then: Essential to the proof was the following result. Let Ω ⊂ C be a domain and let f : Ω → C be analytic. If R is a closed rectangular region in Ω, then f (z) dz = 0.

CAUCHY'S INTEGRAL FORMULA PROOF🔥 EASY METHOD EXPLAINED YouTube
We may view Equation as a special instance of integrating a rational function around a curve that encircles all of the zeros of its denominator. In particular, recalling that Cauchy's Theorem, we find. ∫ q ( z) d z = ∑ j = 1 h ∑ k = 1 m j ∫ q j, k ( z − λ j) k d z = 2 π i ∑ j = 1 h q j, 1. To take a slightly more complicated.

Cauchy's Theorem and Cauchy's Integral Formula YouTube
In applications, the boundary is often only piecewise smooth, and again that is all we need for Stokes. Theorem 4.1. 1: Cauchy-Pompeiu. Let U ⊂ C be a bounded open set with piecewise- C 1 boundary ∂ U oriented positively (see appendix B ), and let f: U ¯ → C be continuous with bounded continuous partial derivatives in U.
Cauchy integral formula YouTube
Cauchy's integral formula states that f(z_0)=1/(2pii)∮_gamma(f(z)dz)/(z-z_0), (1) where the integral is a contour integral along the contour gamma enclosing the point z_0. It can be derived by considering the contour integral ∮_gamma(f(z)dz)/(z-z_0), (2) defining a path gamma_r as an infinitesimal counterclockwise circle around the point z_0, and defining the path gamma_0 as an arbitrary.

Complex Integrals(Cauchy's theorem & Cauchy's Formula) YouTube
UniversityofToronto-MAT334H1-F-LEC0101 ComplexVariables 9-Cauchy'sIntegralFormula Jean-BaptisteCampesato October14th,2020 Contents 1 Simpleconnectedness 1

Cauchy Integral Formula Cauchy Theorem Stock Vector (Royalty Free) 1919090525 Shutterstock
Cauchy's integral formula is a central statement in complex analysis in mathematics. It expresses that a holomorphic function defined on a disk is determined entirely by its values on the disk boundary. For all derivatives of a holomorphic function, it provides integration formulas. Also, this formula is named after Augustin-Louis Cauchy.

An example of Cauchy's Integral Formula Solveforum
We assume C C is oriented counterclockwise. Figure 5.1.1 5.1. 1: Cauchy's integral formula: simple closed curve C C, f(z) f ( z) analytic on and inside C C. (CC BY-NC; Ümit Kaya) Then for any z0 z 0 inside C C: f(z0) = 1 2πi ∫C f(z) z −z0 dz f ( z 0) = 1 2 π i ∫ C f ( z) z − z 0 d z. This is remarkable: it says that knowing the.

Cauchy integral formula 4 examples YouTube
18.04 S18 Topic 4: Cauchy's integral formula. Resource Type: Lecture Notes. pdf. 295 kB 18.04 S18 Topic 4: Cauchy's integral formula Download File DOWNLOAD. Course Info Instructor Dr. Jeremy Orloff; Departments Mathematics; As Taught In Spring 2018.

Cauchy's Integral Formula 1, Proof YouTube
Physics 2400 Cauchy's integral theorem: examples Spring 2017 and consider the integral: J= I C [z(1 z)] 1 dz= 0; >1; (4)where the integration is over closed contour shown in Fig.1.

Cauchy integral formula in complex plane. Download Scientific Diagram
Cauchy's Integral Formula is a fundamental result in complex analysis.It states that if is a subset of the complex plane containing a simple counterclockwise loop and the region bounded by , and is a complex-differentiable function on , then for any in the interior of the region bounded by , . Proof. Let denote the interior of the region bounded by .Let denote a simple counterclockwise loop.
cauchy integral theorem Liberal Dictionary
4 Cauchy's integral formula 4.1 Introduction Cauchy's theorem is a big theorem which we will use almost daily from here on out. Right away it will reveal a number of interesting and useful properties of analytic functions. More will follow as the course progresses. If you learn just one theorem this week it should be Cauchy's integral.

Cauchy's Integral Formula with Examples Complex Integration Complex Analysis 14 YouTube
Theorem 6: Medium Value theorem of Gauss. In the same conditions as Cauchy's integral formula, it is fulfilled. f(a)= 1 2π ∫2π 0 f(a+reiθ)dθ f ( a) = 1 2 π ∫ 0 2 π f ( a + r e i θ) d θ. The proof of this fact is easy, it is enough to observe that in the Cauchy's integral formula we parametrize C.