PPT 6.5 Factoring Cubic Polynomials PowerPoint Presentation, free download ID2795627

Whenever you factor a polynomial (cubic or otherwise), you are finding simpler polynomials whose product equals the original polynomial. Each of these simpler polynomials is considered a factor of the original polynomial. For example, the binomial x ² - 100 has two factors (x + 10) and (x-10). Why?

How to Factor a Cubic Polynomial 12 Steps (with Pictures)

7 Answers Sorted by: 11 By the Rational Zero Theorem all the rational roots of x3 − 12x + 9 x 3 − 12 x + 9 must have a numerator which is a factor of 9 9 and a denominator which is a factor of 1 1. Therefore they have to be of the form 9 1 = 9 9 1 = 9 or 3 1 = 3 3 1 = 3. Let f(x) =x3 − 12x + 9 f ( x) = x 3 − 12 x + 9.

How to Factor a Cubic Polynomial 12 Steps (with Pictures)

This algebra 2 and precalculus video tutorial explains how to factor cubic polynomials by factoring by grouping method or by listing the possible rational zeros of the polynomial and then.

Factoring By Grouping Factoring By Grouping X^3

The three methods we use for factoring a cubic polynomial are splitting terms using the ad-method, finding a factor by applying the rational root theorem, and cubic formulas for sum, difference, etc. Jump to Questions Irreducible Polynomials Polynomials like 2x + 1 or 3x 2 − x + 1 cannot be factorized. These are irreducible polynomials.

How To Factor A Cubic Polynomial Cubic Equation Wikipedia / In this video we learn a more

Factoring a Cubic Polynomial - Algebra I BroandSisMathClub 18.4K subscribers Subscribe Subscribed 4.8K views 8 years ago In this video, you will learn how to factor a cubic polynomial. A.

How To Factor A Cubic Polynomial How to Factor a Cubic Polynomial 12 Steps (with Pictures

1 Group the polynomial into two sections. Grouping the polynomial into two sections will let you attack each section individually. [1] Say we're working with the polynomial x 3 + 3x 2 - 6x - 18 = 0. Let's group it into (x 3 + 3x 2) and (- 6x - 18) 2 Find what's the common in each section. Looking at (x 3 + 3x 2 ), we can see that x 2 is common.

Cubic Formula Factoring / Factoring Special Binomials You can use the cubic formula, but it is

The goal of this free guide on how to factor polynomials is to give you plenty of step-by-step practice with factoring polynomials—including polynomials with 4 terms (cubic polynomials)—so that can become more comfortable with factoring all kinds of polynomials.

Factor Solve These Cubic Equations In Less Than A Minute Otosection

Factoring cubic polynomials is a process of finding the factors of the cubic polynomials. We can find the factors of a cubic polynomial using different methods such as long division, trial and error method, etc. The factors can be linear, quadratic, or cubic (if it does not have any roots).

Factoring Cubic Trinomials 24 best images about Binomial & Trinomial on Pinterest Montessori

Factoring by Grouping This is by far the nicest method of the two, but it only works in some cases. Consider the polynomial p(x) = x3 4x2 + 3x 12: We group the rst two terms and the last two terms together: p(x) = (x3 4x2) + (3x 12) and then we pull out the common factors: p(x) = x2(x 4) + 3(x 4): Notice now that these two terms now have x

How to Factor a Cubic Polynomial 12 Steps (with Pictures)

The cubic polynomial formula is in its general form: ax 3 + bx 2 + cx + d a cubic equation is of the form ax 3 + bx 2 + cx + d = 0. The values of 'x' that satisfy the cubic equation are known as the roots/zeros of the cubic polynomial. Let us see how to find them in different ways. How to Solve Cubic Equation?

Factoring a Cubic Polynomial Algebra I YouTube

Factoring Cubic Polynomials Brody Acquilano , Patrick Corn , Ahmed Kamel , and 1 other contributed A cubic polynomial is a polynomial of the form f (x)=ax^3+bx^2+cx+d, f (x) = ax3 +bx2 +cx+ d, where a\ne 0. a = 0. If the coefficients are real numbers, the polynomial must factor as the product of a linear polynomial and a quadratic polynomial.

PPT 6.5 Factoring Cubic Polynomials PowerPoint Presentation, free download ID2795627

The first step to factoring a cubic polynomial in calculus is to use the factor theorem. The factor theorem holds that if a polynomial p (x) is divided by ax - b and you have a remainder of 0 when it's expressed as p (b/a), then ax - b is a factor. It's a roundabout way of saying that if an expression divides evenly into a polynomial.

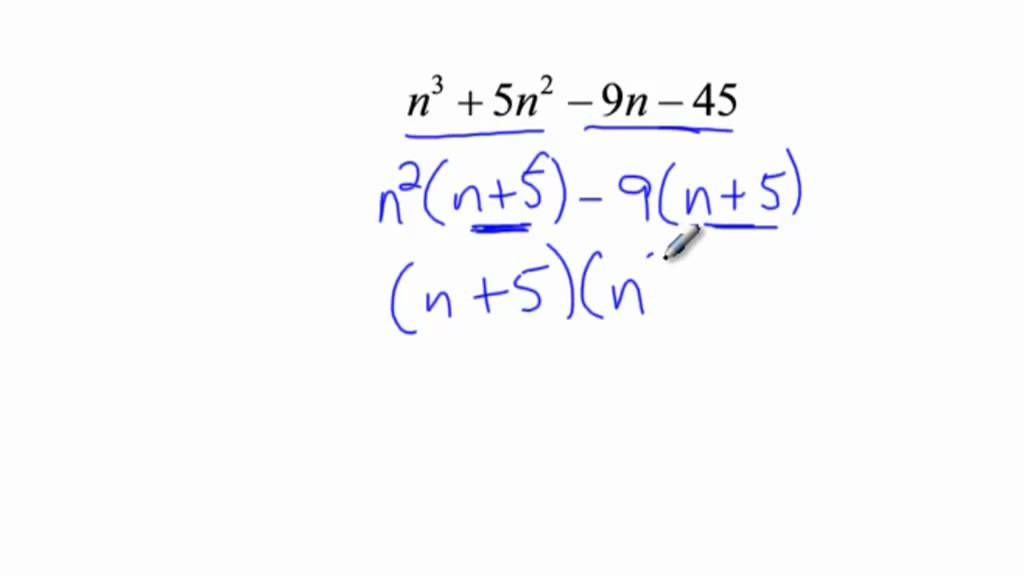
How To Factor Cubic Polynomials How to Solve Equations that are Not Perfectly Cubed Video

Factoring difference of cubes (video) | Khan Academy Algebra (all content) Course: Algebra (all content) > Unit 10 Factoring difference of cubes Math > Algebra (all content) > Polynomial expressions, equations, & functions > Advanced polynomial factorization methods © 2024 Khan Academy Terms of use Privacy Policy Cookie Notice

Algebra II Ch55 Part B Factoring Cubic Polynomials YouTube

To find the factored form of a polynomial, this calculator employs the following methods: 1. Factoring GCF, 2 Factoring by grouping, 3 Using the difference of squares, and 4 Factoring Quadratic Polynomials Method 1 : Factoring GCF Example 01: Factor 3ab3 −6a2b 3ab3 −6a2b = 3 ⋅a ⋅b ⋅b ⋅ b−2 ⋅ 3 ⋅a ⋅ a⋅ b = = 3ab(b2 −2a) solve using calculator

How To Factor A Cubic Polynomial With Three Terms Solution When Does This Cubic Equation Have

Factoring Cubic Polynomials Robert G. Underwood 1. Introduction There are at least two ways in which using the famous Cardano formulas (1545) to factor cubic polynomials present more diﬃcul-ties than the quadratic formula poses when factoring quadratic polynomials. First and obviously, with its cube roots and roots of

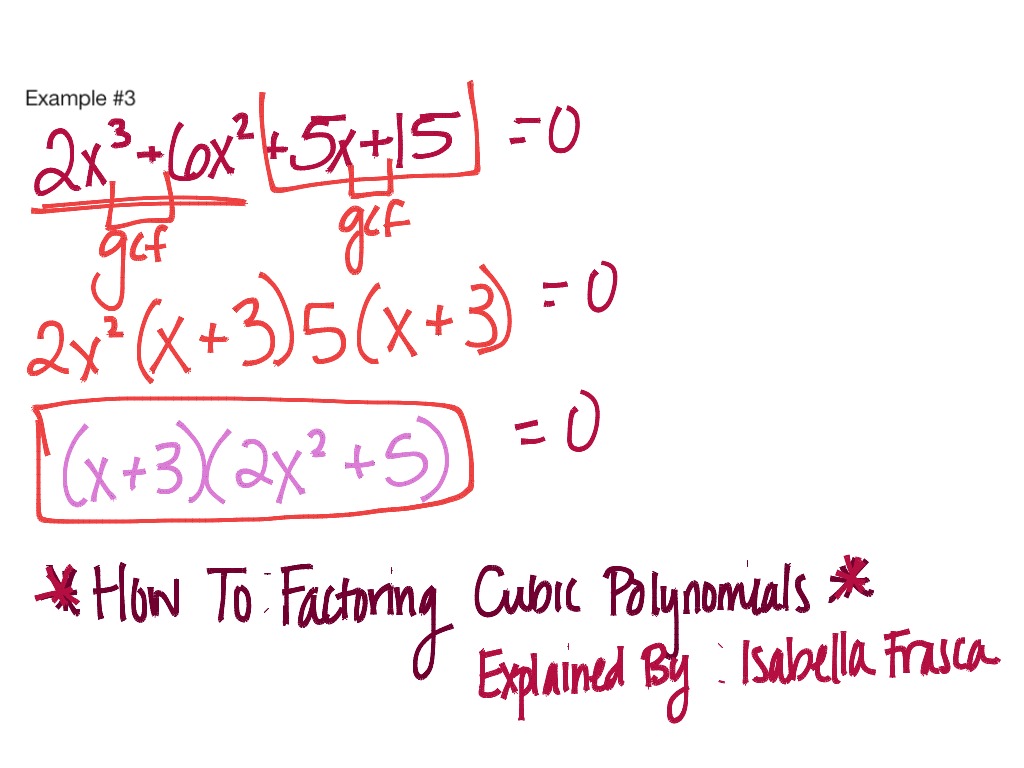
Factoring Cubic Polynomials Math, Algebra 2 ShowMe

If you are factoring a polynomial and run into an irreducible quadratic, just leave it alone. The irreducible quadratic would be considered one of the factors of the polynomial. Factoring Cubic Functions.. Example \(\PageIndex{12}\): Factoring a Cubic Function. Completely factor the function \(f(x)=x^3+8x^2+21x+18\).